【導讀】本文提出了一種預測IC熱性能的方法。這些信息對于汽車及其它高溫環境下使用的PMIC (電源管理IC)尤為有用。通過分析熱性能,我們設計了一種數學模型用于仿真芯片內部的瞬態溫度。我們引入了關于熱性能的物理定律,并用于評估IC的發熱模型。基于這些分析,我們提出了一種等效的無源RC網絡,用于仿真IC瞬態熱性能的模型。為了闡述這一分析的應用,我們設計了一個用于LED驅動(MAX16828)的RC網絡。最后總結了這種方法的使用和有效性,并提出了加速構建RC模型的途徑。
設計人員通常需要了解IC的熱性能,特別是汽車應用中的PMIC (電源管理IC)。當實際IC工作在高溫環境(例如+125°C)時,是否會觸發熱關斷電路或超出產品的安全工作溫度范圍? 如果沒有明確的分析方法,我們就無法確切地回答這一問題。因此,在定義一款新IC時,我們需要一種根據復雜的內部功能預測熱關斷或管芯溫度過高的方法。
直流工作模式下,往往能夠利用數據資料提供的參數確定結溫,例如θJA (熱阻)和θJC (結溫熱特性)1。然而,為了預測直流模式以外的結溫峰值達到多高(例如,由PWM信號驅動的功率MOSFET,用于控制LED或開關穩壓器),需要了解瞬態熱特性數據。盡管該數據非常有用,但通常情況下數據資料并未提供該數據。您可能還需要了解芯片在給定功率耗散水平下能夠工作多長時間而不發生故障。這個問題也很難回答。
本文解決了利用功耗和環境溫度預測芯片結溫的問題,芯片結溫是時間函數。本文首先引入分析方法所依據的物理定律。然后將IC系統定義為一個復雜的分層熱體模型進行討論。進而對熱體模型進行理論分析,并得出瞬態熱性能的表達式。本文根據這些公式提出了一種等效的RC無源網絡,用于表示IC的熱特性。最后,為了證明這一分析方法的有效性和準確性,文章給出了具有PWM調光功能的高電壓線性HB LED (高亮度LED)驅動電路MAX16828的實驗結果。
熱力學定律
對于任何物體,均可通過以下兩個基本定律得到溫度與時間的關系式。
牛頓冷卻定律:
其中:
- TB為物體溫度。
- TA為環境溫度。
- kA為比例常數(> 0)。
- t為時間。
根據能量守恒定律:
其中:
- P為熱源產生或傳遞給熱源的恒定功率。
- m為發熱體質量。
- c為特定物體的熱容量。
結合這兩個定律,我們得到:
IC的數據資料通常列出了封裝的熱特性數據,例如θJA。我們利用該數據可以分析封裝的穩態熱平衡,從而檢查是否滿足式3:
穩態時式
因此:
P = mckA(TB - TA) (式4)
可將式4轉換為:
其中:
- θBA為物體至環境的熱阻。
- TB為封裝內溫度。
- TA為外部環境溫度。
故:
將芯片定義為一個熱系統
清晰地定義系統非常重要,因為熱分析結果依賴于這一定義。從安裝在PCB的芯片橫截面(圖1),我們可以看到管芯到環境通道至少有三種不同材料:管芯本身、環氧樹脂鑄模和封裝。根據主要熱源的位置不同,熱模型基于兩種熱流動模式之一:從外部熱源至管芯(當外部熱源是主要熱源時)和從管芯至外部環境(當管芯為主要熱源時)。我們就這兩種模式分別進行討論。
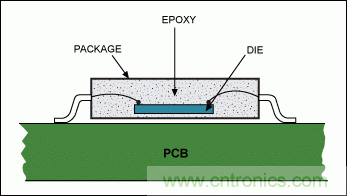
圖1. 安裝在PCB上的芯片橫截面,顯示了管芯和環境之間的材料層次。
從外部熱源至芯片的熱流動
考慮圖2所示系統,該圖給出了一個均勻物體從電源獲得能量(熱量)并向外部環境釋放能量的示意圖。
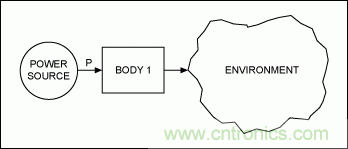
圖2. 該熱模型說明了從外部電源至芯片(組件1)然后再返回到環境的熱流動。
熱量通過封裝和鑄模復合物到達內部管芯。所以,該系統也模擬了熱源處于封裝外部時芯片的瞬態熱特性。由于管芯具有很多金屬,封裝熱阻通常比管芯本身高得多。因此,管芯溫度隨著封裝溫度的變化而改變,幾乎沒有滯后,使芯片看起來像個整體。我們可以利用式3定義這一整體系統。求解TB,得到:
其中,ko為積分常數,由初始條件求解得到。一般而言,該式對于熱源處于芯片外部情況下定義芯片的瞬態熱特性非常有用。
可以通過一個實例解釋這一模型。確定芯片的瞬態熱特性,其初始溫度為Ti,式7中帶入t = 0,TB = Ti:
因此:
考慮Ti = TA的特殊情況:
利用式6,可將式9和式10改寫為:
式11和式12在熱源處于封裝外部情況下,對于預測芯片溫度(無論是封裝還是管芯)非常有用。需要耗散大量熱量的大電流MOSFET附近就是一個熱源特例。
已知kA和θJA,即可計算出不同時間的溫度。或者,如果P為時間的復合函數,即可利用以上公式作為時間仿真來評估溫度,并利用MATLAB®軟件編程繪制溫度隨時間變化的函數。
θJA由數據資料提供。但是,如果某項配置條件與JEDEC標準規定不同,利用公布的θJA值進行計算會產生誤差。JEDEC標準51-3節指出:“值得強調的是,利用這些測試板測試得到的數值不能用于直接預測任何具體應用系統的性能,只能用于封裝之間的比較”2。所以,為了正確估算溫度,應該針對原型開發板測量θJA值,或按照下列說明直接估算。
從管芯至環境的熱流動
考慮圖3所示的三體系統(與芯片相似),在管芯處產生熱量并通過環氧樹脂和封裝將熱量耗散至外部環境。組件1為管芯,組件2為環氧樹脂,組件3為芯片封裝。
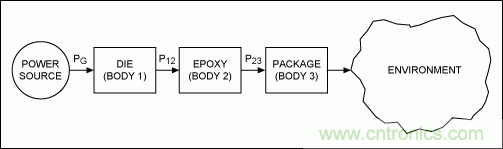
圖3. 三體模型與圖2所示模型的比較。此時,管芯產生的熱流動更為復雜。
為了求解該系統中的θJA,我們必須為三個物體定義公式。
組件1:
組件2:
組件3:
其中:
- TB1、TB2和TB3分別是組件1、2和3的瞬時溫度。
- P12是以熱形式從組件1傳導至組件2的功率。
- P23是以熱形式從組件2傳導至組件3的功率。
- PG是組件1直接產生的功率,或直接傳導至組件1的功率。
管芯產生的功率(PG)減去管芯吸收的功率,得到:
環氧樹脂接收到的功率減去環氧樹脂吸收的功率,得到:
將式16和式17代入式13、式14和式15:
從式18、式19和式20求解三體系統比較復雜,但利用拉普拉斯變換可以簡化計算。求解公式為:
TB1 = T1em1t + T2em2t + T3em3t + TA + (θ12 + θ23 + θ3A)PG (式21)
其中:
- θ12為組件1至組件2的熱阻。
- θ23為組件2至組件3的熱阻。
- θ3A為組件3至環境的熱阻。
- T1、T2和T3為積分常數。
- m1、m2和m3為k1、k2和k3的函數。
管芯產生功耗時,式21能夠以非常準確的方式預測管芯溫度。然而,使用該式時,我們必須知道所有積分常數以及m1、m2和m3,它們為復雜函數,求解非常困難。為了避開這種困難操作,我們利用一個工具求解不同方程:SPICE。
RC網絡模型瞬態熱特性的微分方程
現在,我們提出一個類似的微分方程,用作電路建模,我們對電路進行仿真,并通過仿真得到溫度讀數。
微分方程18、19和20可通過代表管芯產生功率的RC簡單網絡(圖4)進行模擬。
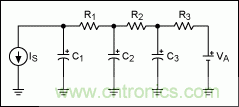
圖4. 該RC網絡用于仿真內部產生熱量時芯片的瞬態熱特性
圖4中,電容的初始電壓分別表示管芯(C1)、環氧樹脂(C2)和封裝(C3)的溫度。VA表示環境溫度,IS (流入電容C1的電流)表示管芯產生的功率。表示電容電壓的差分方程為:
這三個方程式對應于式18、式19和式20,用以下變量替換:
電容電壓與管芯、環氧樹脂和封裝的溫度直接相關。任何SPICE工具包均可方便地仿真RC電路。若已知具體芯片模型的R1、R2、R3、C1、C2和C3的適當參數,即可對該電路進行仿真,并直接以電容C1電壓的形式讀取管芯溫度。
現在,我們可以確定具體芯片的無源元件值(R1、R2、R3、C1、C2和C3)。通過測量管芯最終的穩態溫度,利用式5 (以下改寫為式25)得到系統的熱阻(θJA):
其中:
- TJ為管芯的穩態結溫。
- TA為環境溫度。
- PG為管芯的耗散功率。
工作在與式25相同的耗散功率(PG)下,從時間0開始,不同時間測量的管芯溫度可以構成反映管芯瞬時溫度變化的一組數據。然后,根據以下約束條件,對于實測數據進行曲線擬合,可以確定R1、R2、R3、C1、C2和C3值:
θJA = R1 + R2 + R3 (式26)
測量管芯溫度
有幾種測量集成電路管芯溫度的方法3。這里,我們將采用ESD二極管正向壓降測量法確定芯片溫度,因為這一方法簡單且不會引入大的誤差。但是,為了保證測量誤差在可以接受的范圍內,需要針對具體芯片謹慎選擇管芯溫度的測量技術。實踐證明,遵循以下原則非常關鍵3。
確保選擇用于測量的ESD二極管沒有很大的寄生電阻,也不會流過大電流,以免造成二極管壓降讀數偏差。最好與IC制造商討論確定內部焊線和金屬電阻的最大估算值。
還要確定ESD二極管接近芯片熱源或處于實際考慮管芯溫度的區域內。這種配置能夠更好地估算溫度,獲得更準確的結果。
若選擇FET的導通電阻估算溫度指示,請確保FET在測試溫度下完全導通,并處于最小壓降。
利用ESD二極管正向壓降進行測量時,需要芯片上的二極管作用了正向偏壓,對其電壓進行測量。大多數芯片很容易做到這點,將ESD二極管連接在引腳與電源電壓之間即可。因為實測數據為二極管壓降,還必須考慮二極管電壓與溫度之間的關系式4。
二極管電壓以接近恒定的斜率下降,偏差可以忽略不計。如果繪制隨溫度變化的曲線,可以得到類似于圖5的結果。
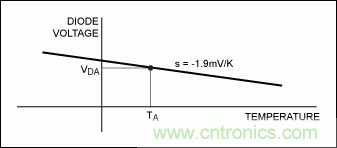
圖5. 固定電流偏置下,二極管正向壓降隨溫度的變化關系。
圖5中,TA為環境溫度,VDA為環境溫度下的二極管電壓,由此,我們得到曲線上的一個點及斜率。在溫控爐內不同溫度點對二極管電壓進行測量,即可得到斜率。或采用一個常見數值:2mV/K,該值在各種二極管電流范圍都有效,誤差很小4。這些數值同樣適用其它芯片,但出于準確度的考慮,最好測量對應于二極管偏置電流的斜率。至此,可以利用二級管電壓表示任何溫度:
其中:
- T為二極管電壓VD對應的溫度。
- s為曲線斜率(s < 0)。
將該表達式代入式11和式12,得到下式:
VD = sθJAP + VDA + (VDi - sθJAP - VDA)e-kAt (式28)
VD = VDA + sθJAP(1 - e-kAt) (式29)
代入式18、式19和式20,得到:
為了恰當地將RC網絡用于實測二極管電壓瞬態數據的曲線擬合,我們只需將電流源的幅值設置為:
lS = sPG (式33)
由于s < 0,通過將電流源反向并將其幅值設置為|sPG|即可實現式33。
RC網絡的實驗測定和驗證
我們可利用以上得出的方程式和線性LED驅動器(例如MAX16828/MAX16815)驗證RC仿真模型的實際應用。這些芯片工作在最高40V電壓,幾乎不需要外部元件,MAX16828能夠為一串LED供電,最大電流可達200mA (圖6)。MAX16815與MAX16828引腳兼容,功能相似,但最大輸出電流可達100mA,而非200mA。
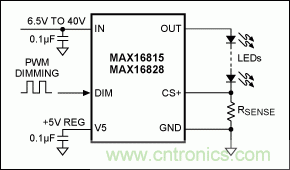
圖6. MAX16815/MAX16828 HBLED驅動器的典型應用電路
兩款LED驅動器都適合于汽車應用,例如,用于側燈、汽車尾燈、背光和指示燈。如果內部MOSFET需要承受較大電流,而且具有較大壓差時,MAX16828將需要耗散相當可觀的熱量(LED串的正向電壓較低時,MOSFET會發生這種情況)。RSENSE兩端的電壓調節在200mV ±3.5%,該電阻用于設置LED電流。芯片的DIM輸入為LED提供較寬范圍的PWM調光,因為它能夠承受高壓,可以直接將其連接到IN引腳。
為了直接顯示管芯溫度,我們對連接在DIM和IN引腳之間內部ESD二極管的正向偏壓進行測量。該二極管偏置在大約100µA,其正向電壓變化率為2mV/K (這點可通過溫控爐對器件加熱進行驗證),實驗設置如圖7所示。5V電源和56kΩ電阻提供100µA偏置電流,為ESD二極管提供正向偏置。驅動器設置為可向LED提供200mA的輸出電流。
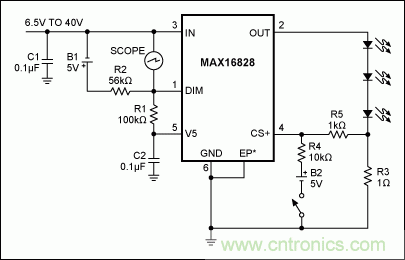
圖7. 圖中所示測試裝置采用片上ESD二極管測量管芯的瞬時溫度,*EP表示裸焊盤。
這種狀態下,元件承載大量電流,ESD二極管測量處于測量通路。因此,由于焊接線和內部金屬電阻的影響,會產生一定誤差。根據內部布局和焊接線長度計算,估計最差情況下的寄生電阻為50mΩ。200mA下,該寄生電阻會在二極管讀數上產生大約±10mV (最大)的誤差,對應的溫度測量精度誤差大于±5°C。此外,管芯ESD二極管放置在靠近片上功率MOSFET和熱保護電路處。這種配置可使二極管更準確地表示該區域的溫度。
系統定義1
接下來的部分介紹如何利用測試裝置,采集代表瞬時熱特性的二極管電壓,用于上述式7和式21的系統定義方程式。
為了計算kA和θJA (代入式11),采用熱風槍加熱芯片。因為我們并不希望芯片內部產生熱量,所以將芯片斷電。利用熱風槍加熱元件會使封裝、管芯的溫度上升。可利用示波器測量二極管的電壓,以監測管芯的溫度變化(圖8)。
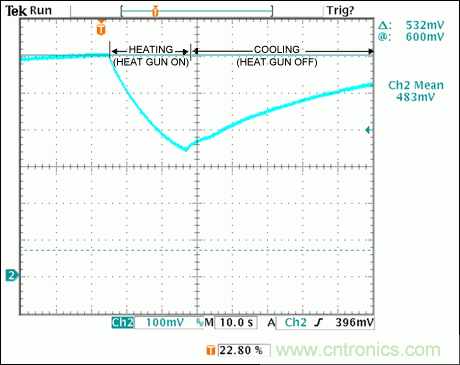
圖8. 該二極管電壓瞬態值包括表示外部熱風槍加熱(下降曲線)和移開熱風槍后冷卻(上升曲線)的指數曲線
當芯片加熱時,二極管電壓按照指數規律迅速下降,與公式預測結果一致。接近曲線中間位置時,關閉熱槍,使封裝和管芯開始冷卻。二極管電壓又按照指數規律上升。
我們并不確切知道有多少熱量從熱風槍傳遞到芯片。因此,為了消除該未知數,我們首先將式28調整為僅擬合曲線(圖8)的上升部分(冷卻)。這種曲線擬合使我們能夠估算kA的最佳值。冷卻期間沒有熱功率傳遞至封裝,封裝僅僅進行冷卻,P = 0。因此,式28可簡化為:
VDB = VDA + (VDi - VDA)e-kAt (式34)
我們已知VDA (室溫下的初始測量值為643mV)和VDi (t = 0時的參考讀數)值。為了確定kA,我們必須調整方程式,使其包括上升曲線的一對讀數,將得到kA = -0.0175。圖9所示為采用上述kA值時的讀數(二極管電壓單位為mV,與以秒為單位的時間的對應關系)和式34的波形。
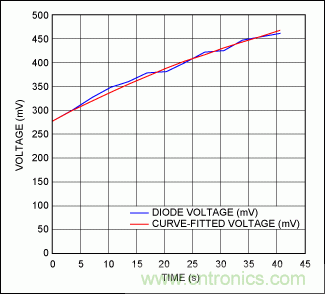
圖9. 式34,擬合至一對二極管電壓測量值,非常接近芯片經過熱風槍加熱后再冷卻的二極管測量值。
正如我們在圖9中看到的那樣,式34與kA = -0.0175時的測量數據非常接近。為了驗證我們公式的正確性,我們嘗試利用針對kA測定的值擬合公式28的下降曲線,方程式精確擬合(圖10)。因此,我們看到針對系統定義1所討論系統的式34與實驗數據非常接近。
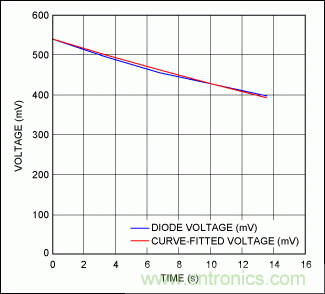
圖10. 式28擬合曲線與曲線下降部分(加熱)的二極管電壓測量值非常接近
系統定義2
驗證系統2的式30、式31和式32更加困難。必須在管芯產生熱量,利用二極管正向電壓測量管芯溫度,并將溫度值與提出的RC網絡的C1電壓仿真數據進行擬合。這項工作可利用MATLAB編程實現。
在已知整個芯片初始溫度的情況下,記錄不同時間的瞬態熱特性非常重要。按照這種方式,我們還可以求解RC網絡的初始電容電壓。利用相同的測試裝置(參見圖7),接通電流通道并在示波器上采集二極管電壓(圖11)。
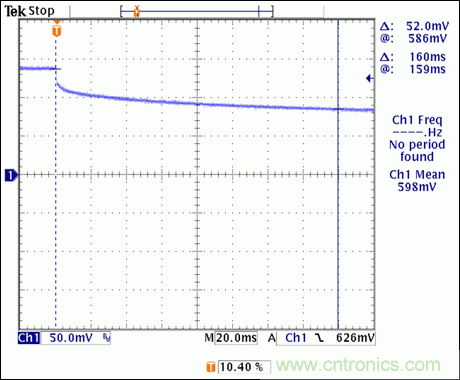
圖11. MAX16828內部二極管的正向電壓瞬態值,表明片上MOSFET已經導通并產生熱量。
記錄三種不同耗散功率下的瞬態電壓,用一條曲線模擬這些數據。圖12所示曲線是第一組數據的擬合結果,此時功耗為1.626W;圖13所示波形是實測數據與仿真數據的比較。同樣,圖14所示波形說明了RC網絡對第二組讀數(耗散功率為2.02W)的仿真;圖15所示波形說明了對第三組讀數(耗散功率為1.223W)的仿真情況。
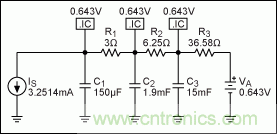
圖12. 采用圖示元件值,該RC網絡能夠仿真由管芯產生熱量時芯片的瞬態熱特性。
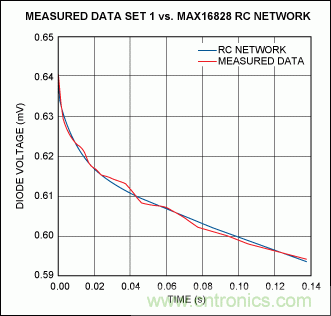
圖13. 當管芯耗散功率為1.626W時,芯片加熱曲線的實測結果與擬合曲線的比較。
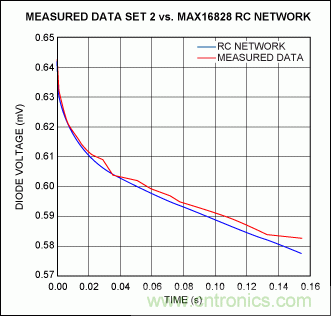
圖14. 當管芯耗散功率為2.02W時,芯片加熱曲線的實測結果與擬合曲線的比較。
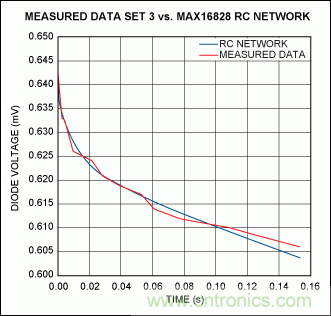
圖15. 當管芯耗散功率為1.223W時,芯片加熱曲線的實測結果與擬合曲線的比較。
實驗結果表明實測結果與理論模型非常吻合。一旦針對具體芯片構建RC網絡模型,這種模型將對仿真IC的瞬態溫度非常有用。模型亦可用于類似尺寸的芯片,確定其定義階段的熱特性。利用這種方式可以表示芯片的工作范圍限制,反過來,這些信息也能夠幫助定義芯片的工作模式,以避免過熱。
結論
本文介紹了通過RC網絡仿真芯片熱特性的方法,然后可以利用SPICE工具方便地進行仿真。以下方法有助于提高該模型的精度:
獲取極端功耗條件和中等水平下的數據。將RC網絡同時擬合到三個不同狀況,使模型復合絕大多數實際功耗的要求。
通過在不同環境溫度下采集數據提高模型精度。
必要時,可以通過實驗提高精度,但大多數應用并不需要知道精確溫度。應用和設計工程師以及系統設計人員會從這種測試方法獲得很大益處。為了得到更詳細的芯片信息,制造商可以為其IC構建RC網絡,并利用芯片的相應SPICE模型進行驗證。
參考文獻
"Package Thermal Resistance Values (Theta JA and Theta JC) for Dallas Semiconductor Temperature Sensors," Maxim application note 3930.
"Package Thermal Characteristics," Actel Corporation application note AC220, (February 2005).
Rako, Paul, "Hot, cold, and broken: Thermal-design techniques," EDN online (3/29/2007).
Pease, Bob, National Semiconductor, "The Best of Bob Pease. What''s All This VBE Stuff, Anyhow?" (11/5/2008).
本文來源于Maxim。
推薦閱讀:







