【導讀】在本文的第一部分,我們討論了當運算放大器用于type-2補償器時,對開環增益AOL的影響。對運算放大器幅值和相位響應的進一步分析,顯示存在低頻和高頻兩個極點。如果在低帶寬設計中可忽略這些極點的存在,那么在高帶寬系統中需要增益和相位增強時就必須考慮它們帶來的失真。第二部分中將討論由于存在這些極點,如何確定type-2補償器的傳遞函數以及它們將怎樣令濾波器性能失真。
運算放大器中的兩個極點
為了穩定運行,運放設計人員實施所謂的極點補償,包括在低頻放置一個極點,使放置第二高頻極點前在頻率fc處的增益下降到1(0dB),通常在2fc.。
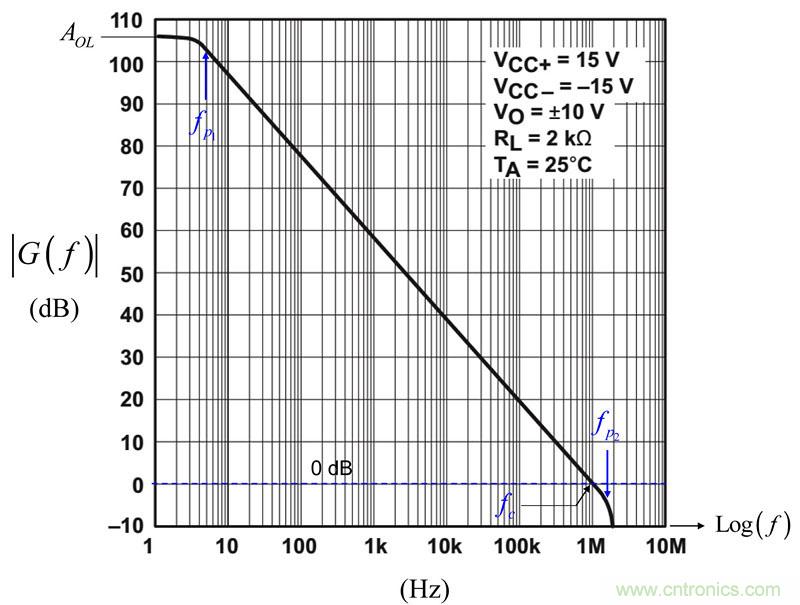
圖1:運放的開環動態響應揭示了兩個極點的存在
圖1所示為一個典型的μA741,您可看到交越頻率1 MHz,低頻極點5 Hz左右,而第二極點出現在2MHz。請注意,這是個典型的響應,開環增益AOL106dB。開環增益不是個精確控制的參數,它可顯著變化。數據表規定在整個溫度范圍內(-55至125°C)增益從15K(83.5分貝)移至200K(106分貝),那么當分立時,這曲線轉變。
一個簡單的拉普拉斯表達式可描述這兩極點開環響應,如圖1所示:
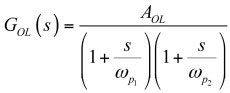 (1)
(1)由圖2的Mathcad?繪制曲線確定:

圖2:運算放大器有一個低頻極點,第二極點在超過0dB的交越頻率處。
運算放大器的一個簡單的SPICE模型
我們可以很容易地建立模仿圖2的頻率響應的SPICE模型。如圖3,它采用一個電壓控制的電流源G1,G1有跨導gm,后連一個接地電阻ROL,再與電容C1并聯。對于ROL,反相引腳Vinv的傳遞函數很簡單:
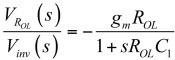 (2)
(2)如果我們現在緩沖電壓,并放置具有電阻R2和電容C2的第二極點,我們得到我們想要的完整的傳遞函數:
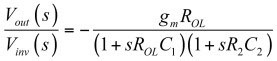 (3)
(3)元件值已自動顯示在頁面的左側,一旦運行仿真,右側就顯示所獲得的幅值/相位圖。這是個簡化的運算放大器模型,但它可以用于第一階分析。它可稍后升級到模型更特定的特點,如電壓鉗位或壓擺率電路,如 [ 1 ] 所描述的。請注意圖中LoL和CoL的存在,由于它們的存在,在元件運行開環時需要將運算放大器輸出電壓固定為2.5 V。這里因為沒有電源軌,我們可運行一個簡單的交流分析,不考慮直流偏置點。
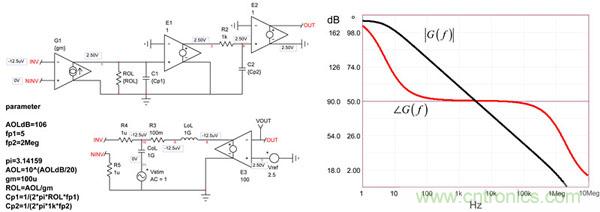
圖3: 一個簡單的SPICE電路,可建立一個有開環增益和兩極點的運算放大器。
然而,如果您打算分析一個包括電源軌的更全面的模型響應,那么當您想要手動調整直流工作點時,這個簡單的電路將避免該集成電路上下波動。在仿真開始時LoL短路,有助于以E3和源Vref調整工作點。一旦交流掃描分析開始于CoL,LoL阻斷E3的調制,調整工作點的電路轉而靜止。這是通常的訣竅,采用平均模型以運行開環增益分析,同時確保確定閉環偏置點到所需的輸出值。這個簡單的SPICE模型將幫助測試我們分析得出的數學表達式。
Type-2補償器有兩極架構
既然我們知道運算放大器有兩個特別的極點,我們可更新在本文第一部分我們最初使用的草圖。圖4所示為新建立的type-2補償器,現在包括運算放大器的內部特征。
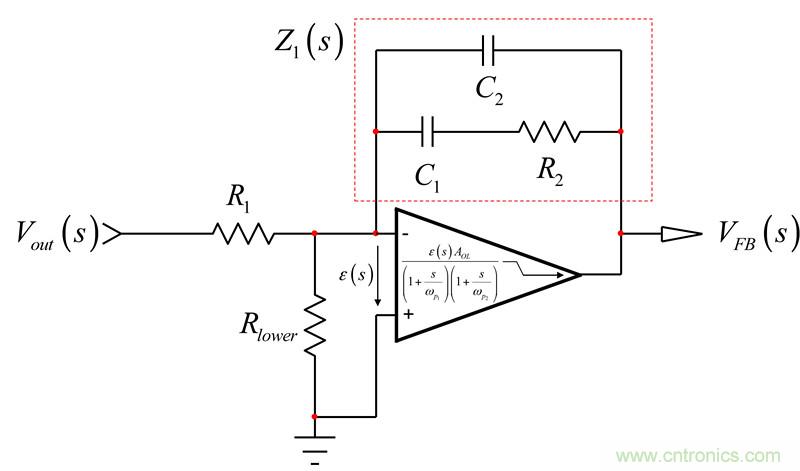
圖4:更新電路將運算放大器中存在的兩個極點考慮進來
輸出電壓VFB是誤差電壓?乘以運放的開環傳遞函數
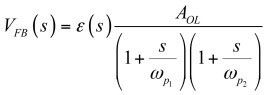 (4)
(4)另外,誤差電壓可通過使用疊加定理將Vout和VFB設置為0V得出:
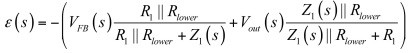 (5)
(5)如果我們將(5)代入(4)并加以整理,得出:
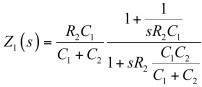 (6)
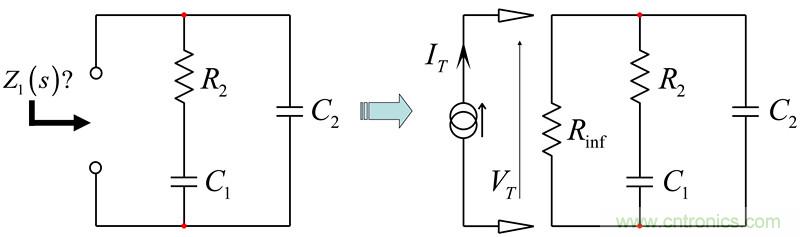
(6)Z1(s)相當于:
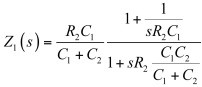 (7)
(7)請參閱本文結尾的附錄,以了解如何用快速分析技術以簡單的步驟推導出這個表達式。
這個方程極其難處理,但有利的是,對于Mathcad?不是問題。我們可通過比較其動態響應與SPICE模型以驗證它是否正確。我們假設下列元件值:
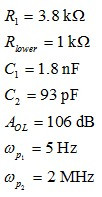
采用type-2架構的SPICE電路如圖5所示。
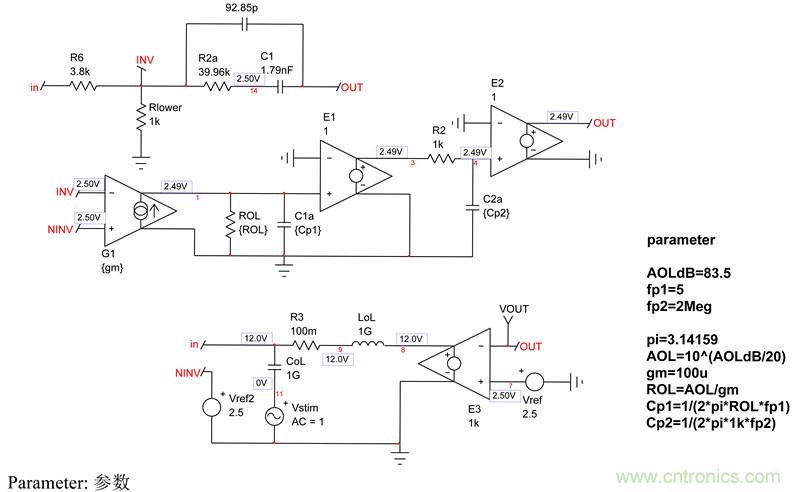
圖5:完整的type-2 SPICE模型現在構成運算放大器的動態響應。請注意,考慮到2.5V參考電壓Vref2現在偏置于NINV引腳,將直流偏置點設置為12V。
由圖6證實,Mathcad?和SPICE之間的響應是相同的,確定方程的有效性。
特征失真
圖5仿真采用的元件值來自一個type-2補償器,旨在以20dB的增益在10kHz交越頻率處建立65°相位增量。如果我們現在比較由本文第一部分方程(36)給出的理想的type-2響應與使用μA741 (106dB AOL,有兩個極點,5Hz和2MHz)的type 2電路的響應,您會注意到一些差異,如圖7所示:
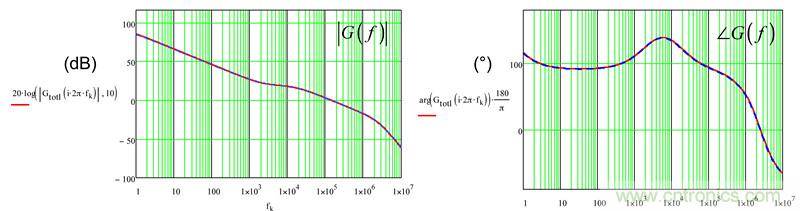
圖6:由Mathcad?提供的繪制曲線與由SPICE產生的曲線完美重合
在該圖中,我們可看到在10kHz處有輕微的增益偏差和離20dB差約2.2dB。其實無關緊要。而更重要的是您以完美的公式實現期望的65°相位增量。在10kHz處,由具有真正運算放大器的電路提供的相位增量僅44.6°或相差20.4°。這將相應減少最終的相位裕量。
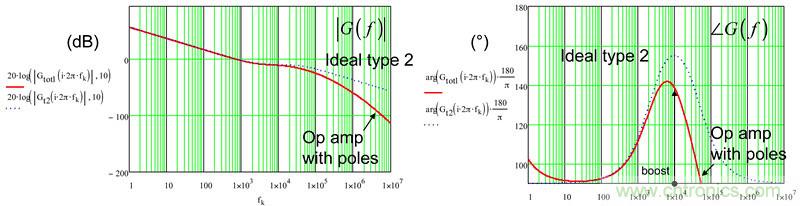
圖7:用有最高開環增益的μA741創建type 2,已導致相位增量失真。
但后面更糟糕。如果您考慮由數據表顯示的開環增益的偏差,若AOL降至83.5dB,最小的規格是多少?圖8證明:在10kHz處的20dB增益差17dB,而相位增量驟降至6.7°。無需解釋為何系統的穩定性與最后一個值有關。圖9的SPICE仿真通過在同一圖中采集的3條不同曲線確定了這些數據。您可看到開環增益偏差的不利影響。
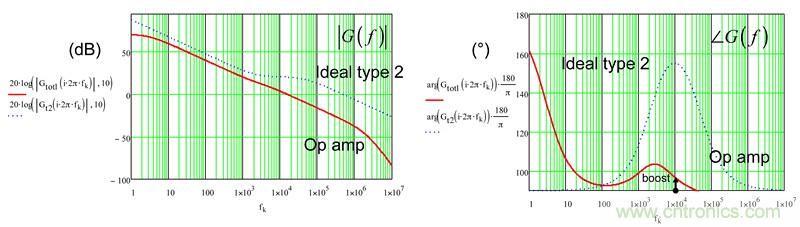
圖8:如果開環增益現在驟降至83.5dB,如運算放大器數據表所述,相位幾乎無提升。
如果我們現在改變type-2規格,也就是說我們在10 kHz處不再需要一個增益,但在fc 處有10dB的衰減,同樣相位增量65°,相位增量失真不那么明顯,開環增益較低(見圖10)。
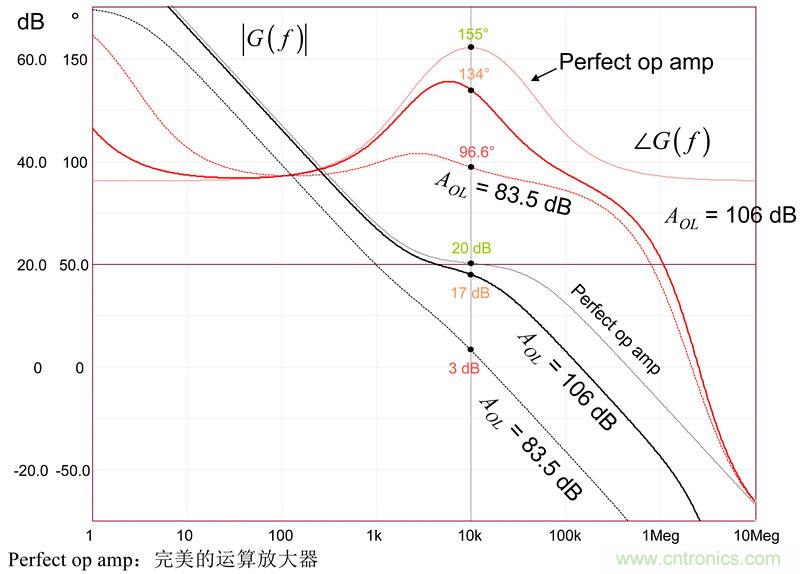
圖9:運算放大器開環增益的變化引起嚴重的增益/相位失真
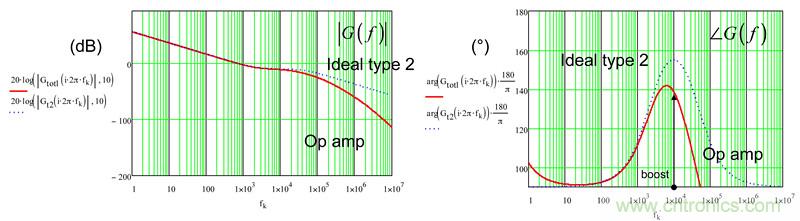
圖10:如果type-2電路改為以10dB衰減而不是在相同的10kHz交越頻率處放大,目標仍沒有達到,但失真程度較小。
采用此架構獲得的中波段增益是-11dB(相對于-10dB的目標),而相位增量剛達到49°(相對于原來的65°目標)。
Type-2響應和開環增益繪制曲線
為確保運放內部不改變補償器響應,通常的建議是在相同的圖線上疊加理論型type 2幅值和運算放大器開環響應。在圖11中,左圖對應于我們第一次嘗試建立的一個type 2補償器,在10kHz處有65°相位增量和20dB增益。在該圖中,運放幅值與type 2補償器相交和相悖,導致我們想要的特征被破壞(最終的相位誤差幾乎有60°)。一看就很明顯,這交叉表明,要么是選擇的運放不適合,要么用type-2補償器設置的目標過高。
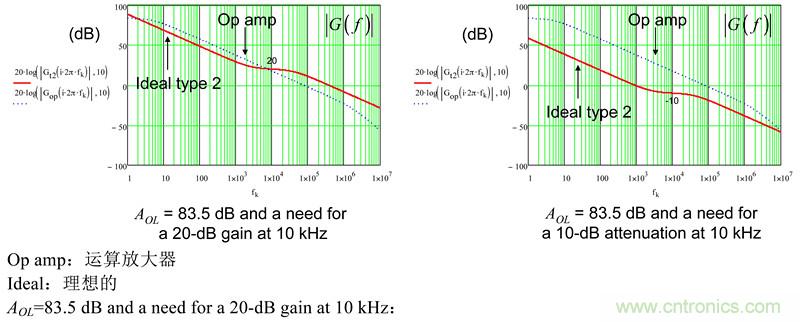
圖11:左圖清楚地顯示這兩個響應相交和衰減。右邊的幅值圖中沒有交叉,但最終的結果也失真。
圖11的右圖似乎表明,我們應當可以設計那樣的type-2電路,在10kHz交越頻率處不再有增益而是衰減。但我們的計算表明不是這樣,因為確定最終有17°相位誤差。
一種方法建議選擇一個增益帶寬乘積(GBW)大于所用type 3補償器的0dB交越頻率的運算放大器。然而您可看到,它不適用于圖11:在左邊,type 2的0dB交越頻率400kHz左右,而在右邊,我們想要衰減而不是增益。我提出一個稍微不同的經驗之談的方案,其中運算放大器的開環響應必須比type 2補償器的20fc “飛高” 20dB。如圖12所示。圖形化的方法是確定你的運放必須具有多少GBW的第一步,以使所需的相位增量和增益目標在可接受的范圍內。
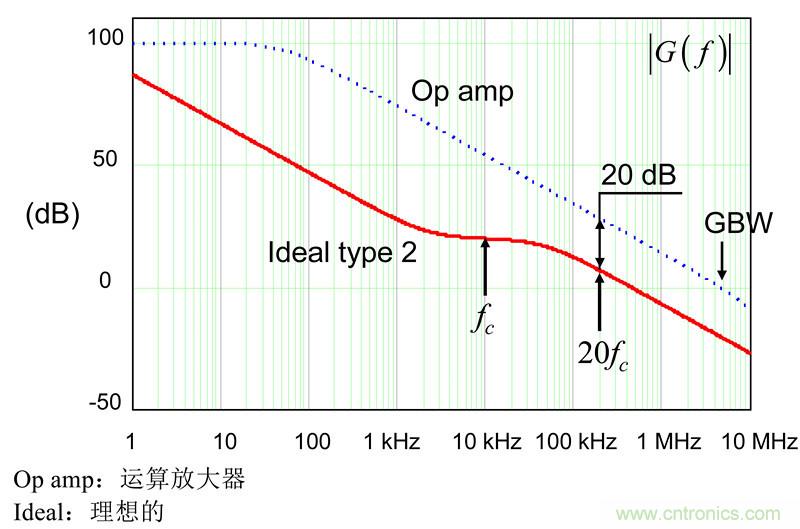
圖12:作為第一步,我們建議選定運放的開環響應至少比type 2補償器的second -1-斜率高20dB。
您首先計算type 2在20fc處的dB幅值,再加20dB。然后您計算出相應的運放開環增益交越頻率或GBW:
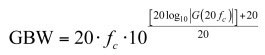 (8)
(8)圖11的左邊,(8)給出了4.4MHz的 GBW,而對第二種情況建議150kHz的GBW。應用這一策略到第一個例子,從而選定運算放大器開環增益為90dB,低頻極點位于150赫茲,或開環增益80dB,低頻極點450赫茲。不要減少開環增益到70dB以下,以使穩態誤差在可接受的范圍內。當應用這種策略,中帶增益為19.5dB,相位增量約60°?。在第二個例子中,(8)建議GBW 140kHz,開環增益80dB和低頻極點15 Hz。中帶增益色散為0.4dB,相位增量為56°或偏差9°。低頻極點增至30赫茲,降低增益色散到0.2dB和相位增量誤差為4.4°。
有了公式(8),您可開始選擇一個合適的運放的GBW。基于觀察和反復實施幾種情況以找到合適的GBW。我曾試圖從(6)提取可能的GBW–例如忽略高頻極點作用–以符合最初完美的type 2特定的偏差,但我不確定已經確立有意義的表達式。一旦您有建議的GBW,就能查找運算放大器的數據表和確定一個合適的元件。將AOL和低頻極點與Mathcad?表[ 3 ]聯系起來,比較與目標的偏差。一定要探索最小值,以致在最壞的情況下偏差仍是可接受的。
高頻電流模式降壓轉換器的補償實例
假設我們設計了一個5A降壓穩壓器,將3.7V電池降至1.5V,開關頻率1MHz。輸出電容是180μF和有3m?等效串聯電阻(ESR)rC。假設我們想要50mV輸出壓降,負載變化從1.5A到5A。因此電源輸出阻抗必須等于:
這可能表明小信號的閉環輸出在交越頻率fc處的阻抗以電容器阻抗為主,其提供的ESR足夠?。?/div>
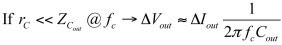 (10)
(10)
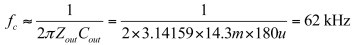 (11)
(11)
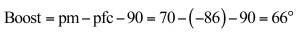 (12)
(12)
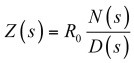 (13)
(13)
 (14)
(14)
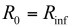 (15)
(15)
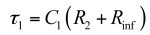 (16)
(16)
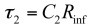 (17)
(17)
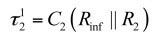 (18)
(18)
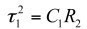 (19)
(19)
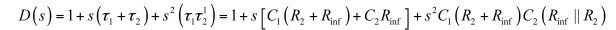 (20)
(20)
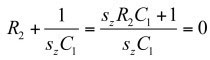 (21)
(21)
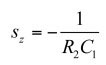 (22)
(22)
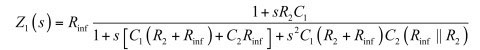 (23)
(23)
 (24)
(24)
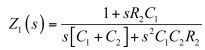 (25)
(25)
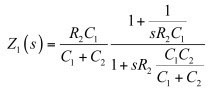 (26)
(26)
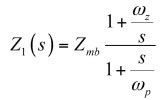 (27)
(27)
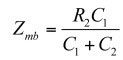 (28)
(28)
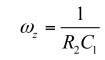 (29)
(29)
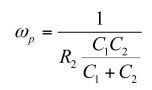 (30)
(30)
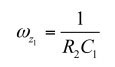 (31)
(31)
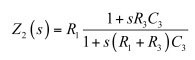 (32)
(32)
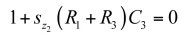 (33)
(33)
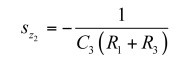 (34)
(34)
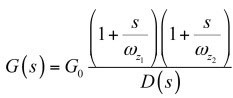 (35)
(35)
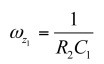 (36)
(36)
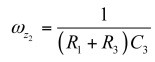 (37)
(37)
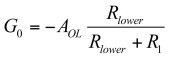 (38)
(38)
從所需的壓降,考慮180μF電容和想要的14.3m?輸出阻抗,我們可估算出需要的交越頻率是:
有些人會反對,認為這是對小信號的近似分析,大信號響應將不同。這是事實,但經驗表明,最終的結果與計算相近。當然,當存在ESR和ESL(寄生電感),結果大大不同,但這第一階的方法是個有意義的起點。此外,此方法分析表明將交越頻率與通常建議的Fsw/5或Fsw/10相比,往往是荒謬的。
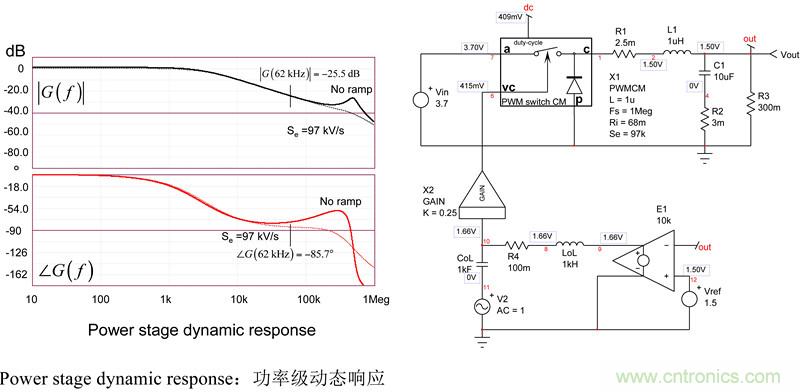
我們選擇了62kHz的交越頻率fc。為了補償這種轉換器,我們首先需要功率級的動態響應,這是分析的出發點。有幾種方式:a)使用控制到輸出的傳遞函數H(s)并由此得出波德圖)b) 用平均模型建立一個仿真設置 c)在實驗室建立一個原型和用網絡分析儀提取響應 或d)用Simplis?或PSIM?建立開關模型和提取交流響應。我們采用了策略b)如圖13所示。

圖13:平均模型幫助我們很快建立電流模式轉換器
從幅值圖,我們看到,如果我們想要62kHz交叉頻率,中頻帶增益必須是25.5dB。如果我們目標是70°相位裕度(pm),在交越處約86°的相位滯后(pfc)需要以下相位增量值:
從Mathcad?表的計算表明,一個極點位于291kHz,而零點將位于13.2kHz。根據(8),必須選擇一個50 MHz的GBW放大器。查閱各種運放的數據表,我們發現LT1208具有典型的7k開環增益(約77dB),可降到2k(66dB)為最小值。其典型增益帶寬積為45MHz,在電源?5V時,降至34兆赫。因此,低頻極點位于34兆赫/7k,約4.8kHz處。

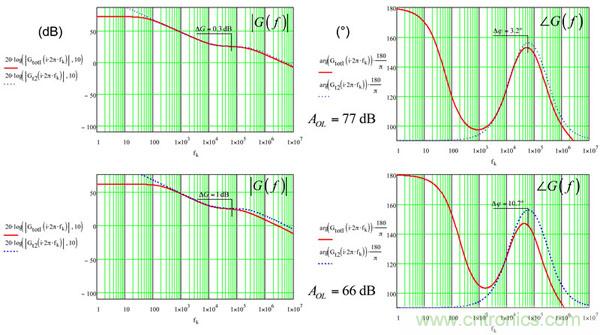
圖14:開環增益色散會影響到最終有效的相位增量
圖14所示為兩個不同的開環增益的type-2波德圖。77dB提供45 MHz GBW和色散很小。當AOL降至66dB(最低規格),增益色散仍可接受,但相位增量偏離目標10.7°。
降壓轉換器中的運放
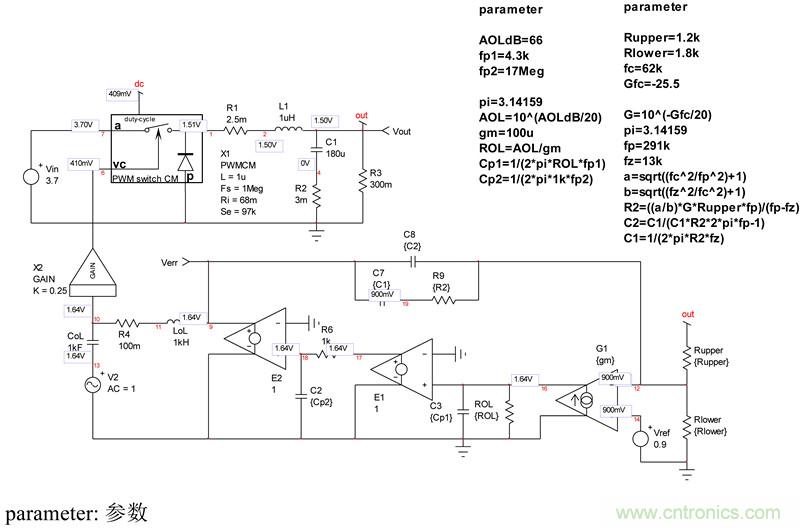
我們現在可以實際模型(至少有AOL與兩個極點)閉環和捕獲選定的運算放大器的特點到我們現在更新的的仿真原理圖。

圖15:運算放大器現在有低頻和高頻兩個極點
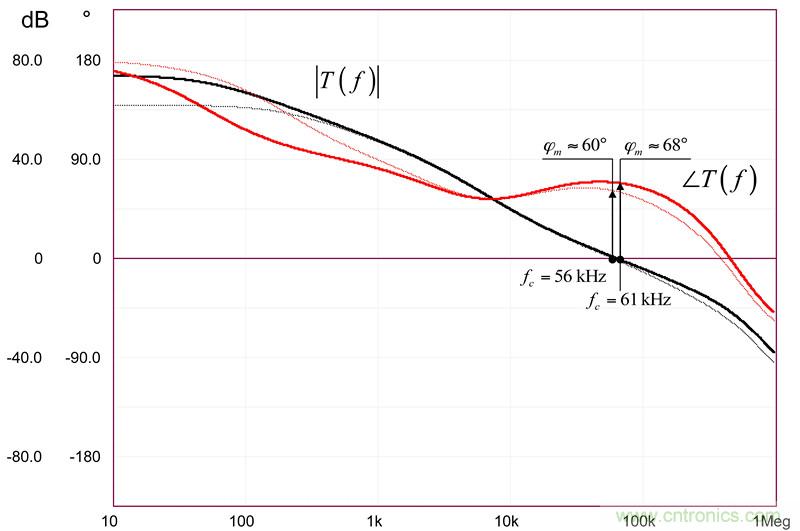
由該圖,我們可繪制開環增益T(f),并看到開環的變化如何影響動態響應。結果如圖16所示。正如預期的那樣,交越頻率和相位裕度出現一些色散。

圖16:動態響應受開環增益變化的影響。在最壞的情況下(66dB AOL),相位裕度下降到60左右°,是可接受的(虛線)。
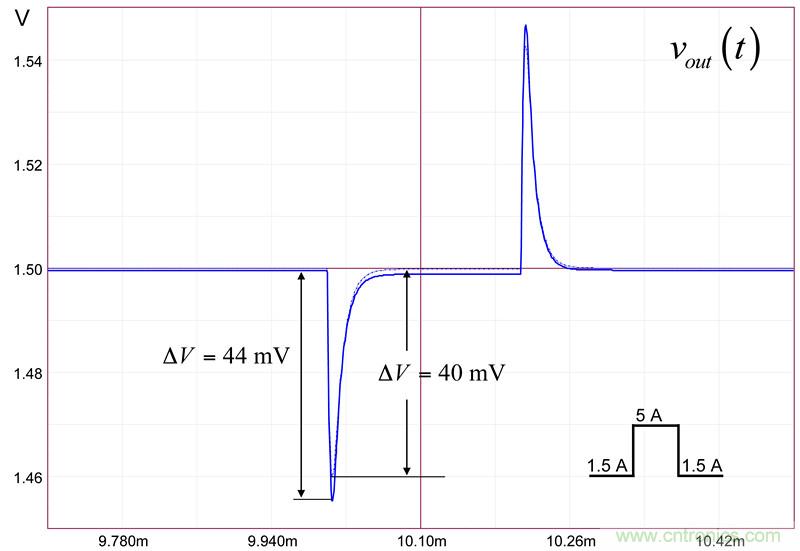
由圖15仿真電路,我們可運行一個瞬態負載階躍,并檢查兩個不同開環增益的響應。結果如圖17所示。

圖17:最低的開環增益有44mV的偏差而典型值導致壓降40mV(虛線對應于66dB AOL)
該壓降在兩個開環增益值的規格范圍內。當然,這是個簡化的方法,考慮到運算放大器的誤差電壓偏差(1.6 V),壓擺率必須是整個分析的一部分,其影響對瞬態響應的評估。
總結
第二部分介紹了運放動態響應對補償器性能的影響。當需要大帶寬時,您不可再忽視這些對補償器的動態響應的作用??梢詫⒛胍耐昝赖膖ype-2響應與所選擇的運放的開環幅值圖疊加,并看看是否重疊。然而,我們已看到的一種情況是,不重疊最終導致一個顯著的相位增量失真。通過運算放大器開環響應和完美的type 2開環響應之間的顯著差距,您可選擇增益帶寬積,并以給定的公式檢查它如何影響所需的響應。一個全面的穩定性分析,必須通過影響所有元件容差考慮整個環路增益,包括運算放大器的內部。通過(6)中完整的type-2傳遞函數,您就可以進一步分析。
附錄 – 阻抗計算
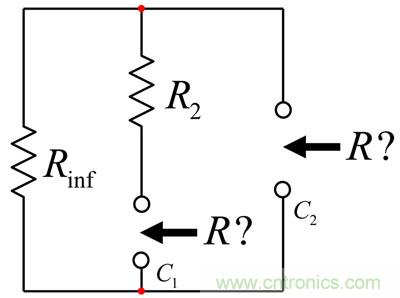
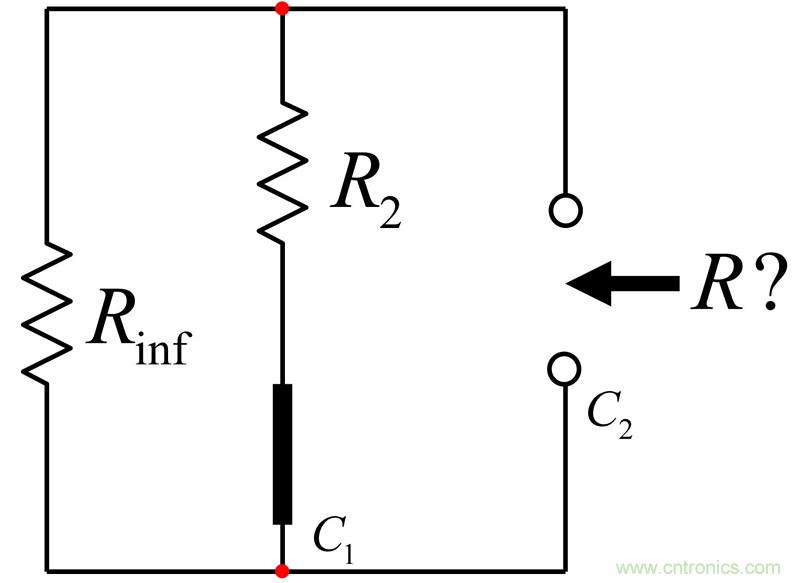
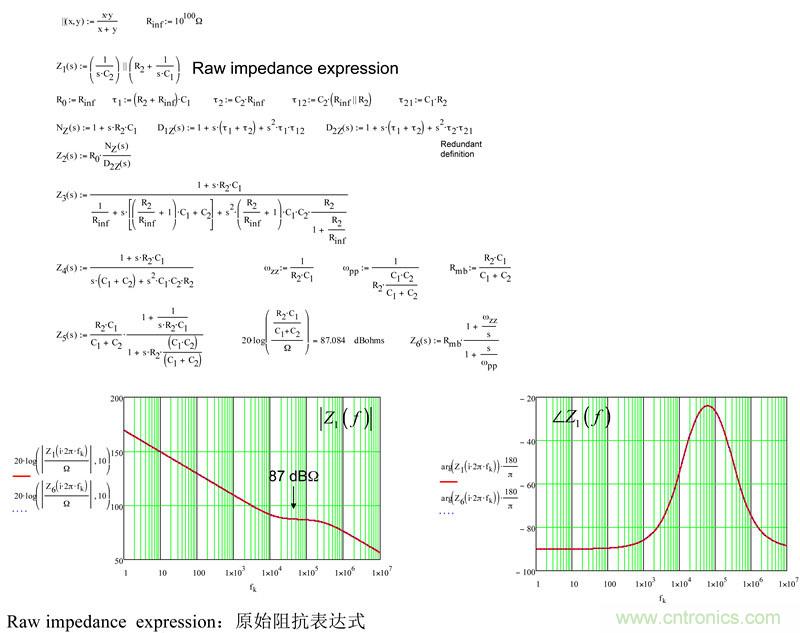
為確定由(7)給出的阻抗,我們可以充分應用快速分析技術。原理圖如圖18所示。為了獲得阻抗,我們將電流源IT注入到電路環路。IT是激勵而VT是響應。我們想要的傳遞函數是將響應與激勵聯系起來的關系。為了便于分析,我們在測量終端裝上了假負載電阻Rinf。我們將馬上看到其中的原理。

圖18:有兩個電容,這是個二階電路。
這類回路的傳遞函數可表示為以下形式:
對于二階系統,我們可以證明分母遵循下列公式:
 (14)
(14)?1和?2是所有儲能元件(C和Ls )保持在直流狀態(電容開路,電感短路)時獲得的時間常數。 表示在時間常數1(上標數字)的元件處于高頻狀態(電容器短路,電感開路),同時確定在時間常數2的元件端的電阻。相反的, 表示在時間常數2(上標數字)的元件處于高頻狀態(電容器短路,電感開路),同時確定時間常數1的元件端電阻。然后將這些時間常數組合,成為如(14)的D(s)。
首先,我們看看S = 0時,儲能元件端的電阻。在直流狀態下,我們讓所有電容開路和電感短路(如果有的話)。在開始任何類型的分析(.TRAN 或.AC)前,確定偏置點時,SPICE也同樣這樣做。我們想象如果我們移除電容器,輸入端阻抗由Rinf決定,因此它的存在避免了無法衡量的項:
然后,我們確定每個電容器端提供的電阻R,而其對應于非直流狀態(斷開或從電路中移除)。我們繪制出圖19。時間常數由?= RC定義。

圖19:您現在評估每個電容器端在直流狀態(從電路中移除)時所提供的電阻
無需寫一行代數,我們就可以檢查圖形和“得出”電容器端的電阻。我們有:
和
有了直流時間常數,讓我們確定更高的頻率,如圖20所示。對于 ,電容C1短路,您看看電容C2端的阻抗。

圖20:電容C1短路,C2端的電阻是多少?
時間常數直接等于:
如果我們評估 ,將發現:
我們將所有項組合形成D(s):
分子可以通過檢驗得出。如果您還記得我在第一部分所說的,當一個特定的S值使變換后的回路無響應(即C替換1/SC)時,會找到零點。在圖18中,響應是VT,由電流源測量。當VT變為0 V,電路中一定出現了轉換的短路。如果是這樣,那么:
如果是這樣,那么:
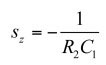 (22)
(22)一切都已妥當,完整的傳遞函數如下所示:
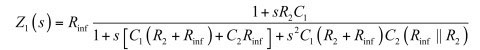 (23)
(23)在分母中,提出Rinf,得到:
 (24)
(24)簡化,令Rinf接近無窮大。最終的表達式為:
如果您現在將分子中的R2C1提出,會得出分子中有倒數的所謂的低熵表達式:
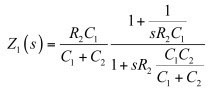 (26)
(26)可用下列公式進一步調整:
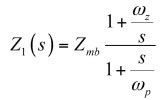 (27)
(27)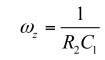 (29)
(29)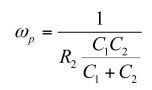 (30)
(30)首項(28)仍然含阻抗,但不再是S=0時的值。它是您在圖21中看到的平坦區或中頻帶電阻,我們匯集所有表達式來測試它們的個別響應。它們都是相同的。

圖21:Mathcad?確定原始表達式和最終表達式相同
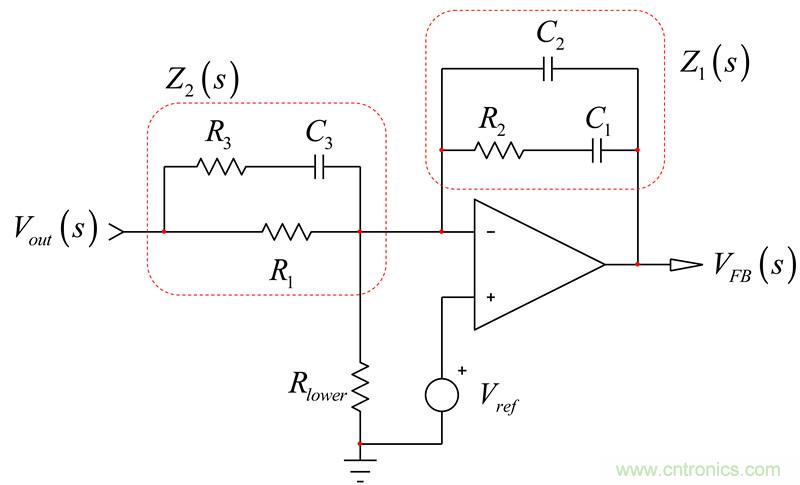
快速分析電路技術展示了如何將電路分解成小的個別的草圖,并單獨解決每個草圖。若可檢測,很快就能得到結果,和得出有條有理的形式。這是這種方法的強大之處,我鼓勵您掌握這技巧,因為在確定復雜的傳遞函數時,時間優勢是很重要的。 為激發您的興趣,請看圖22。您看到一個type-3補償器。無需寫一行代數,我可以告訴您,當Z1和Z2分別轉化為短路和開路時,響應VFB消失。(26)已評估了Z1,并提供一個零點,等于:
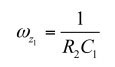 (31)
(31)為了防止激勵Vout形成響應VFB,還有個選擇是Z2開路。換句話說,對于s = sz2,阻抗表達式不再有分母。

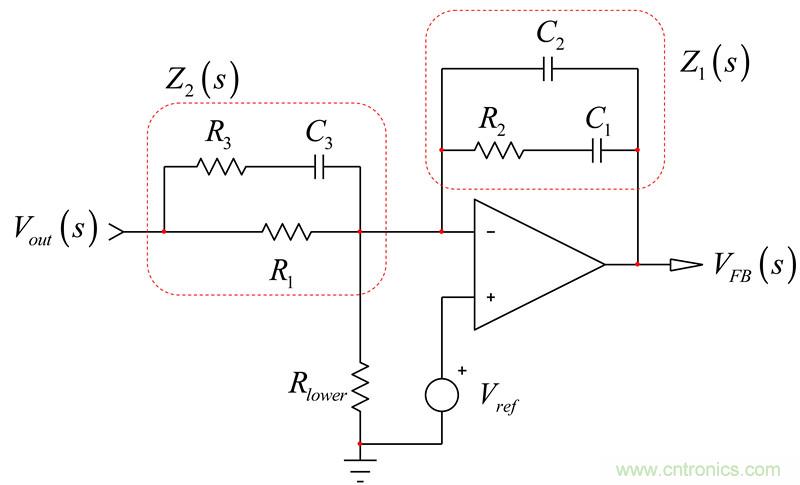
圖22:type-3電路是三階有源濾波器
為確定Z2的阻抗(孤立于整個電路),我們可以想象一個電流源與R1并聯,如圖18的右圖。s = 0時,您“看到”電流源兩端的阻抗是R1(C3處于直流開路狀態)。當激勵(電流源)減至0A(一個0-A電流源從電路消失)時,時間常數是C3兩端的電阻R,數倍于C3。簡單地表示為 。我們不需要分子,因為我們只對分母的根感興趣。然而,如果您也想要分子,那么與我們分析Z1的架構相同。如果R3和C3短路,電流源的響應VT消失。只要組合這些數據,就有:
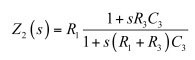 (32)
(32)要取消分母,并讓這個阻抗大小接近無窮大,您必須解得:
從而
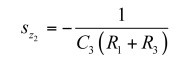 (34)
(34)因此,起媒介作用的type 3傳遞函數是:
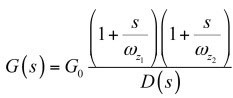 (35)
(35)其中:
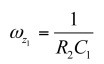 (36)
(36)作者:Christophe Basso,安森美半導體公司
本文來源于電子技術設計。
推薦閱讀:








