【導讀】在第一部分中,我們討論了一般靜態模數轉換器的不精確性誤差和涉及帶寬的ADC不精確性誤差。希望這些內容有助于加深讀者對ADC誤差以及這些誤差如何影響信號鏈的理解?;诖?,要記住的是,并非所有組件都是一樣的——有源和無源器件均是如此,因此,無論系統最終選擇了什么器件,模擬信號鏈中都會存在誤差。
本文將描述精度、分辨率和動態范圍之間的差異。本文還將揭示信號鏈內部的不精確性是如何累積并導致誤差的。定義新設計的系統參數時,這些內容對于理解如何正確指定或選擇一個ADC有著重要作用。
精度、分辨率與動態范圍
許多轉換器用戶似乎在互換使用精度和分辨率這兩個術語,但這種做法是錯誤的。精度和分辨率這兩個術語并不相等,但是具有相關性,所以,不應互換使用??梢园丫群头直媛室暈樘眯置?,但不是雙胞胎。
精度就是誤差,或者說測量值偏離真值的幅度。精度誤差可以稱為靈敏度錯誤。分辨率就是測得值的表示或顯示精細度。即使系統的分辨率為12位,也并不意味著它能測量精度為12位的值。
例如,假設一塊萬用表可以用6位數來表示測量值。則該萬用表的分辨率為6位,但是,如果最后一位或兩位數似乎在測量值之間擺動,則分辨率會受到影響,測量精度同樣會受到影響。 系統或信號鏈里的誤差會一直累積,使原始測量值失真。因此,了解系統的動態范圍也很關鍵,以便衡量要設計的信號鏈的精度和分辨率。
我們再以萬用表為例。如果表示位數為6,則其動態范圍應為120 dB(或6 × 20 dB/十倍頻程)。但要注意的是,最后兩位仍在擺動。因此,真實動態范圍只有80 dB。這就是說,如果設計人員要測量1 µV(或0.000001 V)的電壓,則該測量值的誤差可能高達100 µV,因為實際器件的精度僅為100 µV(或0.0001 V或0.0001XX V,其中,XX表示在擺動的最后兩位)。
實際上,描述任何系統的整體精度的方法有兩種:直流和交流。直流精度表示整個給定信號鏈中展現出來的“偏離”累積誤差,這種方法有時稱為“最差條件”分析。交流精度表示整個信號鏈中累積的噪聲誤差項,這項指標決定著系統的信噪比(SNR)。然后把這些誤差累加起來,結果會使SNR下降,并產生整個設計更真實的有效位數(ENOB)。實際上,取得這兩個參數可以告訴用戶,在靜態和動態信號下,系統有多精確。
低頻SNR、ENOB、有效分辨率和無噪聲代碼分辨率之間的關系
記住,ADC可以“接受”多種信號(通常分為直流或交流),并以數字方式對信號進行量化。了解ADC在系統中的誤差意味著,設計人員必須了解要采樣的信號的類型。因此,信號類型取決于如何定義轉換器誤差對整個系統的貢獻。這些轉換器誤差一般以兩種方式定義:無噪聲代碼分辨率(表示直流類信號)和“信噪比等式”(表示交流類信號)。
由于電阻噪聲和“kT/C”噪聲,所有有源器件(如ADC內部電路)都會產生一定量的均方根(RMS)噪聲。即使是直流輸入信號,此噪聲也存在,它是轉換器傳遞函數中代碼躍遷噪聲存在的原因。其更常用的說法為折合到輸入端噪聲。折合到輸入端噪聲通常用將直流輸入施加到轉換器時的若干輸出樣本的直方圖來表征。大多數高速或高分辨率ADC的輸出為一系列以直流輸入標稱值為中心的代碼。為了測量其值,ADC的輸入端接地或連接到一個深度去耦的電壓源,然后采集大量輸出樣本并將其表示為直方圖(有時也稱為“接地輸入”直方圖)-見圖1。由于噪聲大致呈高斯分布,因此可以計算直方圖的標準差σ,它對應于有效輸入均方根噪聲,表示為LSB rms。
高速模數轉換器精度透視(第二部分)
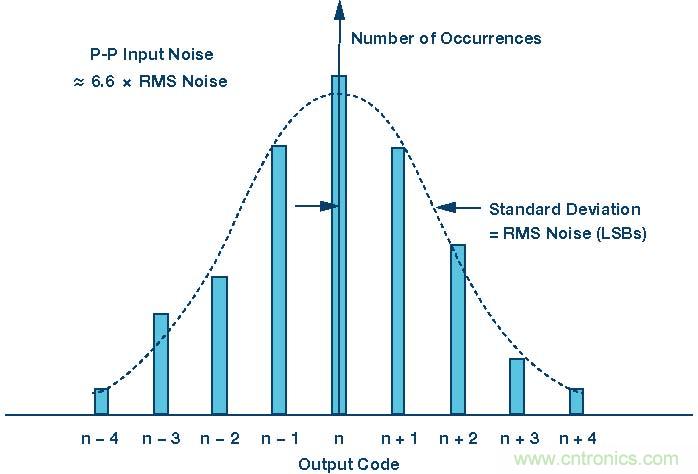
圖1.轉換器折合到輸入端噪聲或ADC“接地輸入”直方圖。
雖然ADC固有的差分非線性(DNL)可能會導致其噪聲分布與理想的高斯分布有細微的偏差,但它至少大致呈高斯分布。如果代碼分布具有較大且獨特的峰值和谷值,則表明存在PC板布局欠佳、接地不良、電源去耦不當等問題。
典型情況下,折合到輸入端噪聲可以表示為均方根量,單位通常是LSB rms。涉及這類量的規格通常與高分辨率精密型轉換器相關,原因在于較低的采樣速率和/或其采集的直流類或低速信號。設計用于精度測量的Σ-Δ ADC,其分辨率在16至24位之間,其數據手冊一般會列出折合到輸入端噪聲、有效分辨率、無噪聲代碼分辨率等規格,用以描述其直流動態范圍。
另一方面,面向音頻應用的較高頻率的Σ-Δ ADC一般都用總諧波失真(THD)和總諧波失真加噪聲(THD + N)來描述。
逐次逼近型(SAR)轉換器涵蓋了廣泛的采樣速率、分辨率和應用。它們通常有折合到輸入端噪聲,但對于交流輸入信號,則還有SNR、ENOB、SFDR和THD等規格。
雖然采樣頻率為數百MHz或以上的高速轉換器(如流水線式轉換器)通常以SNR、SINAD、SFDR、ENOB等交流規格來描述,但它們也能采集直流類信號或低速信號。因此,了解如何從數據手冊上列出的交流規格推算出高速轉換器的低頻性能是非常有用的。
側邊欄討論:SNR等式
理想轉換器對信號進行數字化時,最大誤差為±½ LSB,如一個理想N位ADC的傳遞函數所示。對于任何橫跨數個LSB的交流信號,其量化誤差可以通過一個峰峰值幅度為q(一個LSB的權重)的非相關鋸齒波形來近似計算。對該近似法還可以從另一個角度來看待,即實際量化誤差發生在±½ q范圍內任意一點的概率相等。
圖2更詳細地顯示了量化誤差與時間的關系。一個簡單的鋸齒波形就能提供足夠準確的分析模型。鋸齒誤差的計算公式如下:
e(t) = st, –q/2s < t < +q/2s (1)
e(t)的均方值可以表示為:
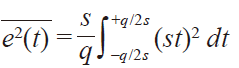 (2)
(2) 進行簡單的積分和簡化可得:
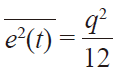 (3)
(3) 因此,均方根量化誤差為: 均方根量化噪聲 =
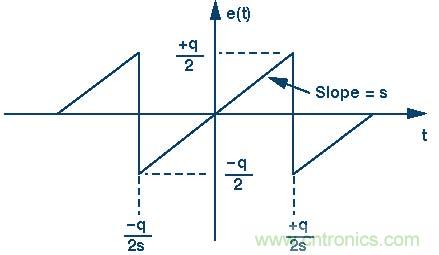
圖2.量化噪聲與時間的關系。
鋸齒誤差波形產生的諧波遠遠超過奈奎斯特帶寬或直流至Fs/2,其中,Fs = 轉換器采樣速率。然而,所有這些諧波都會折回(混疊)到奈奎斯特帶寬并相加,產生等于q/√12的均方根噪聲。
量化噪聲大致呈高斯分布,均勻分布于目標奈奎斯特帶寬上,其范圍通常為直流至Fs/2。這里假設量化噪聲與輸入信號不相關。理論信噪比現在可以通過一個滿量程輸入正弦波來計算:
*滿量程輸入正弦波 *=
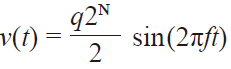 (5)
(5)因此,輸入信號的均方根值為:
滿量程輸入的均方根值 =
因此,理想N位轉換器的均方根信噪比為:
滿量程輸入的均方根值
量化噪聲的均方根值
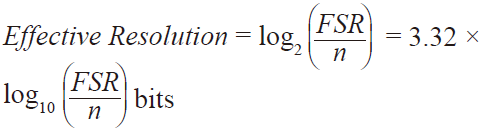 (8)
(8) SNR = 6.02N + 1.76 dB,分布于目標奈奎斯特帶寬。 (9)
要理解低速、直流類信號與高速交流類信號規格量之間的關系,確實需要一些數學知識。所以,請打開大學里用的數學書,翻到后面的標識表。接下來,我們來看看如何理解低頻輸入SNR、ENOB、有效分辨率和無噪聲代碼分辨率之間的關系。
假設FSR = ADC滿量程,n = 折合到輸入端噪聲,則(均方根)有效分辨率定義如下:
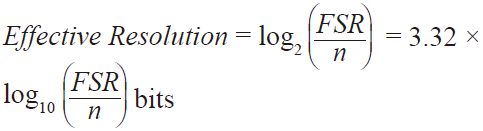 (10)
(10) 有效分辨率
請注意:
log2(x) = log10(x) ÷ log(2) = log10(x) ÷ 0.301 = 3.32 × log10(x) 因此,
 (11)
(11)無噪聲代碼分辨率
或,
無噪聲代碼分辨率 = 有效分辨率 – 2.72 位 (12)
對于交流分析,則要使用滿量程正弦波輸入。另見上面的側邊欄討論,其中:
因此,
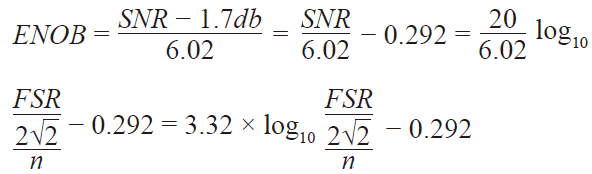 (14)
(14)重新排列后,得到
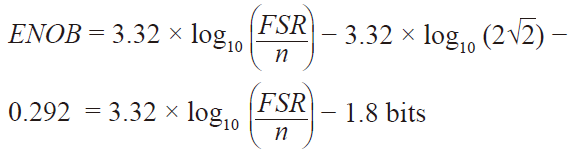 (15)
(15)結果得到下式:
ENOB = 有效分辨率 – 1.5 – 0.292 = 有效分辨率 – 1.8 位 (16)
因此,代入等式16,就可推算出ENOB、交流類信號和直流類(低速)信號之間的關系。或,
ENOB = 無噪聲代碼分辨率 + 2.72 – 1.8 = 無噪聲代碼分辨率 + 0.92 位 (17) 為了驗證這一點,我們來計算一個理想的N位ADC的ENOB。
其中,滿量程范圍(FSR)為 = 2N,且折合到輸入端噪聲為 n = 1/√12 = 0.289。 代入這些值,
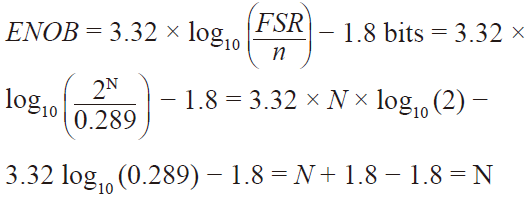 (18)
(18)或,
ENOB = N
總之,對于直流低速信號,系統ENOB約比轉換器的無噪聲代碼分辨率大1位(確切為0.92位),比轉換器的有效分辨率小2位。
然而,隨著信號速率的加快,或者對于涉及帶寬的交流類信號,轉換器的SNR和ENOB會變得與頻率有關,并且在高頻輸入下會下降。
信號鏈中的轉換器不精確性
以上我們了解了轉換器誤差,接下來,我們將討論信號鏈中的剩余部分,以在系統層面了解這些概念。圖3所示為一個簡單的數據采集信號鏈示例。圖中,一個傳感器連傳感器的交流信號先是推過兩級預調理放大器,然后,到達要采樣的ADC輸入端。此處的目的是設計這樣一個系統,使其可以精確地表示傳感器信號,精度保持在傳感器原始值的±0.1%之內。嗯,似乎頗具挑戰性?
為了設計出這樣的系統,有必要思考有哪些類型的誤差可能會影響傳感器的原始信號,還要想想它們來自信號鏈的哪個部分。設想一下,在最終對信號采樣時,轉換器最后會看到什么。
假設在此例中,ADC的滿量程輸入為10 V,分辨率為12位。如果轉換器是理想的轉換器,則可確定其動態范圍或SNR為74 dB。
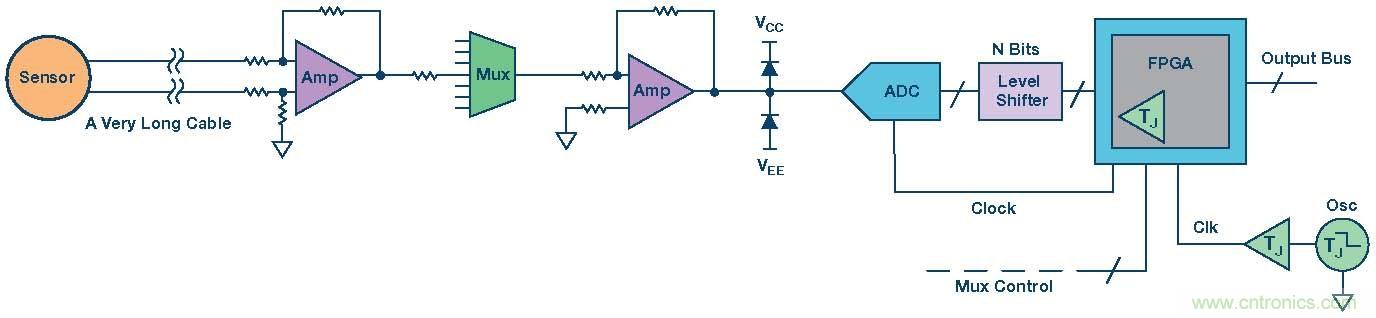
圖3.簡單的數據采集信號鏈。
SNR = 6.02 (12) + 1.76 = 74 dB (19)
然而,數據手冊規格只會顯示,轉換器的SNR為60 dB或9.67 ENOB。
ENOB = (SNR – 1.76)/6.02 = (60 – 1.76)/6.02 = 9.67 位 (20)
請注意SNR和ENOB的計算方法:在用數據手冊中的SNR數據計算ENOB時,設計人員必須明白的是,該數據可能包括,也可能不包括諧波。如果確實包括失真,則可使用SINAD,后者定義為SNR與失真之和,有時稱為THD(總諧波失真)。
因此,LSB大小可以定義為12.2 mV p-p or VFS/2N = 10/29.67。這樣可以大幅減少數據輸出端可能發生的表征的數量。記住,最后的LSB/位因ADC中存在噪聲而擺動!
29.67 = 817 步 (21)
同時意味著,轉換器的精度為±6.12 mV或0.0612%。
(12.2 mV/10 V) × 100 = 0.122% or ±0.0612% (22)
另外,這意味著,如果將1.00000 V的輸入施加到轉換器上,則輸出可能在0.99388 V和1.00612 V之間。
因此,ENOB為9.67位的12位轉換器測量信號的精度只能達0.1%。轉換器的動態范圍約為60 dB而非74 dB(理想的12位ADC)。
0.06% = 0.0006 = 60 dB (23)
此值可以直觀地表示為下面的圖4。

圖4.記住,20 dB/十倍頻程,或3 × 20 = 60 dB。
表1列出了一些簡單的等值換算,供確定目標系統性能時參考。
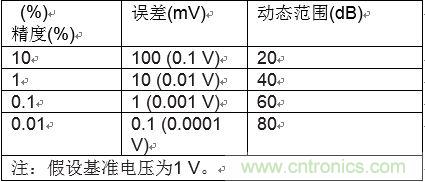
表1:精度等值
其他系統不精確性
要注意上面的信號鏈示例中建議的全部前端組件。正因為轉換器精度達到或超過系統定義的系統精度規格,所以,還有更多的不精確性要理解——即前端、電源、任何其他外部影響或環境。
如上圖3所示,這種信號鏈的設計可能非常復雜,超過了本文討論的范圍。但可以對與這種信號鏈相關的不精確性/誤差進行簡單總結,如表2所示。
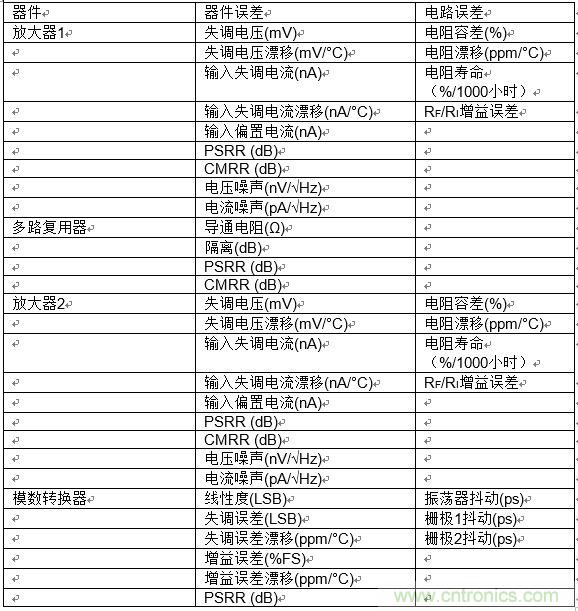
表2:圖3所示信號鏈的累積誤差
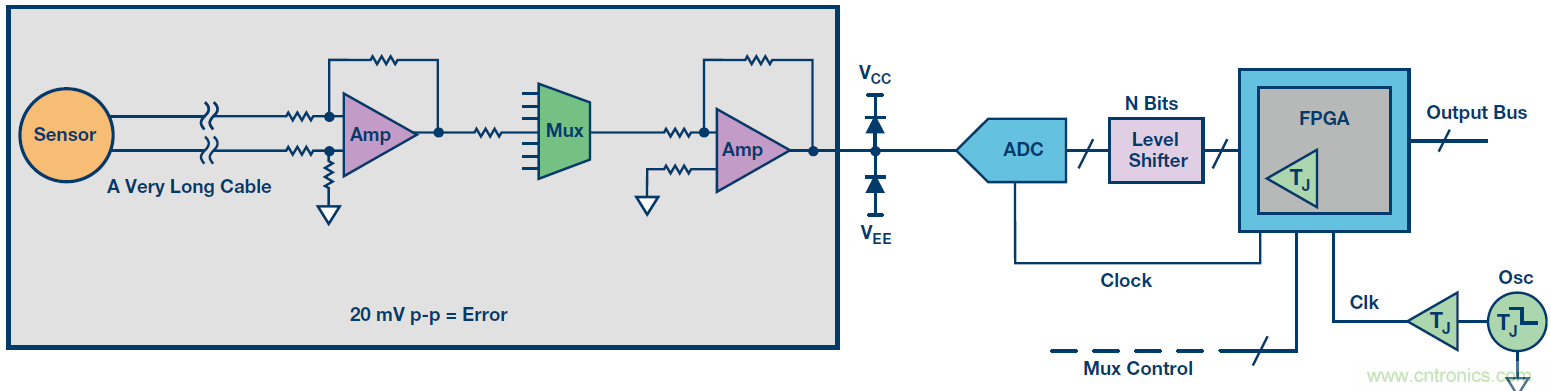
圖5.前端噪聲已定義的簡單數據采集信號鏈。
在任何信號鏈里都存在許多誤差,更不用說電纜和其他外部影響,這些因素也可能在很大程度上決定著這種系統的設計。無論累積誤差怎樣,最終都會與信號一起在轉換器端被采樣——假設誤差不會大到能屏蔽被采樣信號的程度!
在用轉換器進行設計時,要記住,對于系統精度的定義,等式包括兩個部分。一是上面描述的轉換器本身,二是用來在轉換器之前調理信號的所有組件。記住,每丟失1位,動態范圍就會減少6 dB。推論就是,每獲得1位,系統靈敏度就會增長2倍。因此,前端要求的精度規格要遠遠高于用于對信號采樣的轉換器精度。
為了展示這一點,我們采用與圖3所示相同的前端設計。假設,前端本身的不精確性為20 mV p-p;即是圖5所示累積噪聲。系統精度仍然定義為0.1%。同樣的12位轉換器,其精度能否達到定義的系統規格要求?答案是不能,原因如下。
以下是其計算方法,其中所用ADC的SNR = 60 dB。
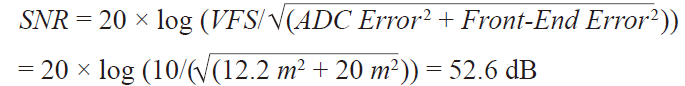 (24)
(24) ADC誤差 前端誤差
注意,20 mV的噪聲可使系統靈敏度下降1位或6 dB,使系統性能從要求的60 dB降至54 dB。為了解決這個問題,可能應該選擇一種新型轉換器,以便維持60 dB或0.1%的系統精度。我們選擇一款ADC,其SNR/動態范圍為70 dB,或者,其ENOB為11.34位,看看是否有用。
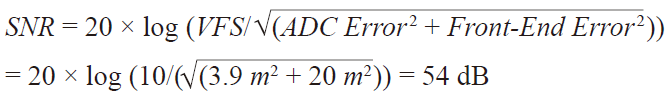 (25)
(25) ADC誤差 前端誤差
看起來性能并無多大變化。為什么?因為前端的噪聲太大,無法實現0.1%的精度,雖然轉換器的性能本身要遠遠好于規格要求。需要改變前端設計,以便實現需要的性能。這種情況如下面的圖6所示。知道最后一個配置示例為什么不起作用嗎?設計人員并不能簡單地選擇一款更好的ADC來提高系統的整體性能。
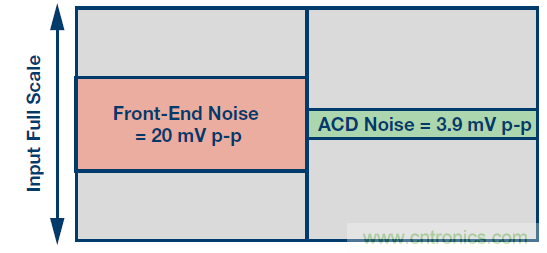
圖6.前端噪聲與12位70 dB ADC噪聲比較。
加總情況
前面選擇的10 V滿量程、12位ADC的動態范圍為60 dB,可實現0.1%的精度。這意味著,總累積誤差需要小于10 mV或10 V/(1060/20),才能達到0.1%的精度要求。因此,必須更換前端組件,以把前端誤差降至9 mV p-p,如圖7所示,所用轉換器的SNR為70 dB。
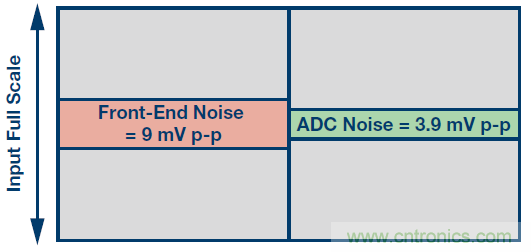
圖7.低前端噪聲與12位70 dB ADC噪聲比較。
如果要使用14位、74 dB ADC,如圖8所示,則對前端的要求甚至可以進一步放寬。但這種折衷可能會導致成本增加。這些折衷要根據具體的設計和應用進行評估。舉例來說,更值得的做法可能是加大對容差更小、漂移更低的電阻的投入,而不是投資采購性能更強的ADC。
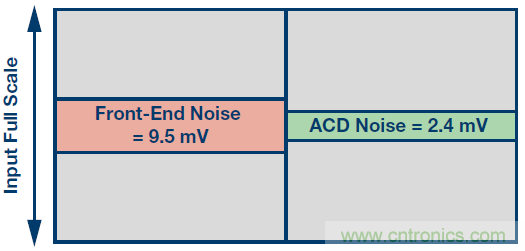
圖8.前端噪聲與14位74 dB ADC噪聲比較。
分析總結
前文簡要介紹了精度誤差、分辨率和動態范圍之間的關系,這些指標為針對具體應用選擇轉換器提供了不同的參考,這些應用則要求達到一定的測量精度。了解所有組件誤差以及這些誤差對信號鏈的影響至關重要。注意,并非所有組件均生而平等!創建囊括所有這些誤差的電子表是插入不同信號鏈組件的簡便方法,可更快進行評估并決定組件的權衡取舍,如表2所示。在不同組件的成本之間進行權衡時,尤其如此。另外,有關如何生成這種電子表格的討論將在本系列第三部分進行。最后,請記住,單純增加信號鏈中轉換器的性能或分辨率無法提升測量精度。如果依舊存在同樣數量的前端噪聲,精度將不會得到改善。只會讓這些噪聲或不精確性測量達到更精細的程度,并最終可能讓設計人員的老板付出更多的成本。
推薦閱讀:







