【導讀】ADC廣泛用于各種應用中,尤其是需要處理模擬傳感器信號的測量系統,比如測量壓力、流量、速度和溫度的數據采集系統……任何設計中,理解這些類型應用的總系統精度始終都是非常重要的,尤其是那些需要對波形中極小的靈敏度和變化進行量化的系統。
理想情況下,施加于信號鏈輸入端的每一個伏特都由ADC以數字表示一個伏特的輸出。但是,事實并非如此。所有轉換器和信號鏈都存在與此相關的有限數量誤差。本文揭示了轉換器內部的不精確性累積到何種程度即會導致這些誤差。定義新設計的系統參數時,若測量精度極為重要,那么這些內容對于理解如何正確指定一個ADC有著重要作用。
ADC的不精確性
無論何種信號鏈,轉換器都是系統的基本要素。為設計選擇的任何ADC都會決定系統的總精度。換言之,系統精度不可能高于轉換器的最低有效位(LSB)大小。為了表明這一點,讓我們來看一個簡短的ADC不精確性指南。
首先,注意到由于ADC不是理想的,并且分辨率有限,因此它們在輸出端只能顯示有限數量的信息表示。表示的信息數量由轉換器滿量程輸入除以2N表示,N為轉換器的理想位數。
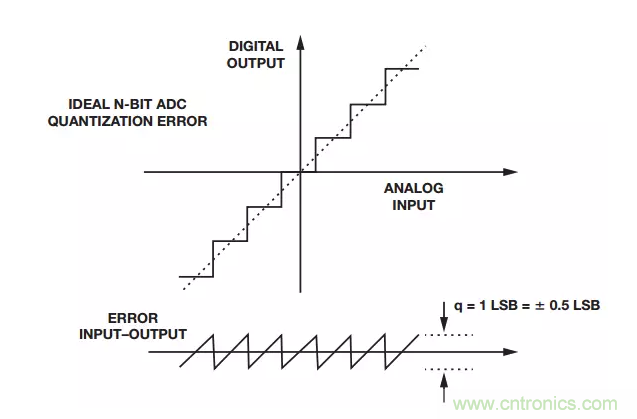
圖1. ADC量化誤差
例如,假設選擇一個12位ADC,則它可在輸出端以4096個數字表示施加于轉換器輸入端的任何信號。這些表示信息確實存在有限量的誤差。因此,如果12位ADC的輸入滿量程(VFS)為10 V p-p,那么其理想情況下的LSB大小為2.44 mV p-p,精度為±1.22 mV。
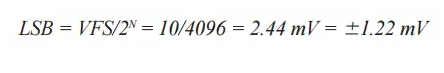 (公式一)
(公式一)而實際上,ADC是非理想的。在轉換器內部存在一定噪聲, KT/C甚至直流中也有噪聲。記住,1 k?電阻等效于4 nV?Hz (1 Hz帶寬,25°C)。注意,查看12位ADC數據手冊時,SNR通常為大約70 dB到72 dB。但是,根據下列公式,一個12位ADC理想情況下應當具有74 dB:
因此,實際上12位分辨率是無法達到的,因為轉換器本身存在一定的不精確性,如圖2所示。
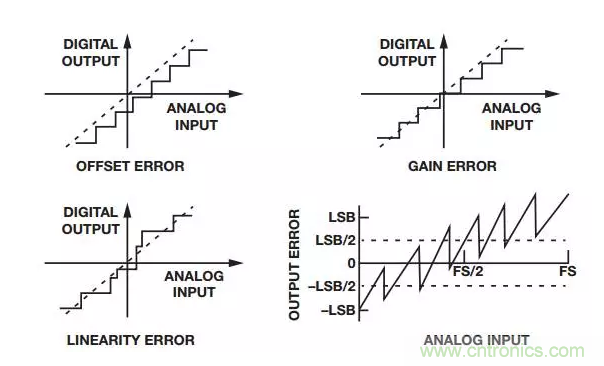
圖2. ADC的不精確性
這些不精確性或誤差決定了轉換器表示信號的效率,并最終為信號鏈所接收。失調誤差定義為傳遞函數無法通過零點的模擬值。增益誤差是失調誤差為零時理想與實際傳遞函數之間的滿量程數值之差。通常意義上的線性度誤差或非線性度是指零電平與滿量程之間的直線偏差,如圖1所示。
有關ADC不精確性的更多信息
對最基本的模數轉換器誤差進行定義并有所了解后,再說明這些誤差的區別會有些幫助。大部分ADC的失調和增益都存在這種小誤差,通常可以忽略或通過外部模擬電路調節(消除),或者采用數字技術校正。然而,諸如線性度、量化和溫度系數等其他誤差無法輕易調節或消除。
模數轉換器線性度只與轉換器自身有關,即取決于架構和工藝變化。有很多方法可以校正,但都很昂貴。設計人員有兩種選擇:
購買更好、成本更高的轉換器,或采用數字手段校正線性度,數字校正的成本也十分高昂,這意味著可能需要更多資源來指定DSP或FPGA,因為線性度會隨溫度和工藝的變化而改變;
根據采樣速率、IF和分辨率,數字校正可能需要廣泛的特性表述和查找表,以便即時校正或調節ADC的性能。
線性度有兩種類型的誤差:它們是差分非線性和積分非線性, 通常分別稱為DNL和INL。
DNL定義為偏離理想值的一切誤差或偏差。換言之,它表示兩個相鄰代碼的模擬差與理想代碼值VFS/2N之間的偏差。可將其看作與ADC的SNR性能相關的因素。隨著代碼的偏差越來越大,轉換數也隨之下降。該誤差在溫度范圍內的界限為±0.5 LSB,可保證無失碼。
INL定義為零電平和滿量程之間的理想直線近似曲率偏差。多數情況下,INL決定了ADC的SFDR性能。INL總偏差形狀可以決定最主要的諧波性能。比如,INL曲線呈弓形會相應產生更差的偶次諧波,而INL曲線呈S弓形則通常產生奇次諧波。該誤差本質上與頻率有關,并與這類誤差分析無關。
哪怕可以消除靜態失調和增益誤差,與失調和增益誤差有關的溫度系數將會依然存在。
例如,一個12位ADC具有10 ppm增益誤差,或FSR/°C = 0.001%/°C。12位系統中的1 LSB為¼096,或者近似等于0.024%。
因此,若125°C ? (–40°C至+85°C),則產生±2.5 LSB增益溫度系數 誤差,或0.001% × 125 = 0.125%,其中,0.125/0.024 = 5.1或±2.55 LSB。
對于失調溫度系數,5 ppm失調誤差或FSR/°C = 0.0005%/°C。
這將產生±1.3 LSB失調溫度系數誤差,或 0.0005% × 125 = 0.0625。其中,0.0625/0.024 = 2.6或±1.3 LSB。
原標題:快進來,今天我們談談ADC的不精確性
(來源:亞德諾半導體)








