【導讀】我們已經(jīng)指出,噪聲比一些較大噪聲源少三分之一至五分之一的任何噪聲源都可以忽略,幾乎不會有誤差。此時,兩個噪聲電壓必須在電路內的同一點測量。要分析運算放大器電路的噪聲性能,必須評估電路每一部分的噪聲貢獻,并確定以哪些噪聲為主。為了簡化后續(xù)計算,可以用噪聲頻譜密度來代替實際電壓,從而帶寬不會出現(xiàn)在計算公式中(噪聲頻譜密度一般用nV/√Hz表示,相當于1 Hz帶寬中的噪聲)。
如果考慮下圖1中的電路——由一個運算放大器和三個電阻組成的放大器(R3代表節(jié)點A處的源阻抗),可以發(fā)現(xiàn)六個獨立噪聲源:三個電阻的約翰遜噪聲、運算放大器電壓噪聲和運算放大器各輸入端的電流噪聲。每個噪聲源都會貢獻一定的放大器輸出端噪聲。噪聲一般用RTI來規(guī)定,或折合到輸入端,但計算折合到輸出端(RTO)噪聲往往更容易,然后將其除以放大器的噪聲增益(非信號增益)便得到RTI噪聲。
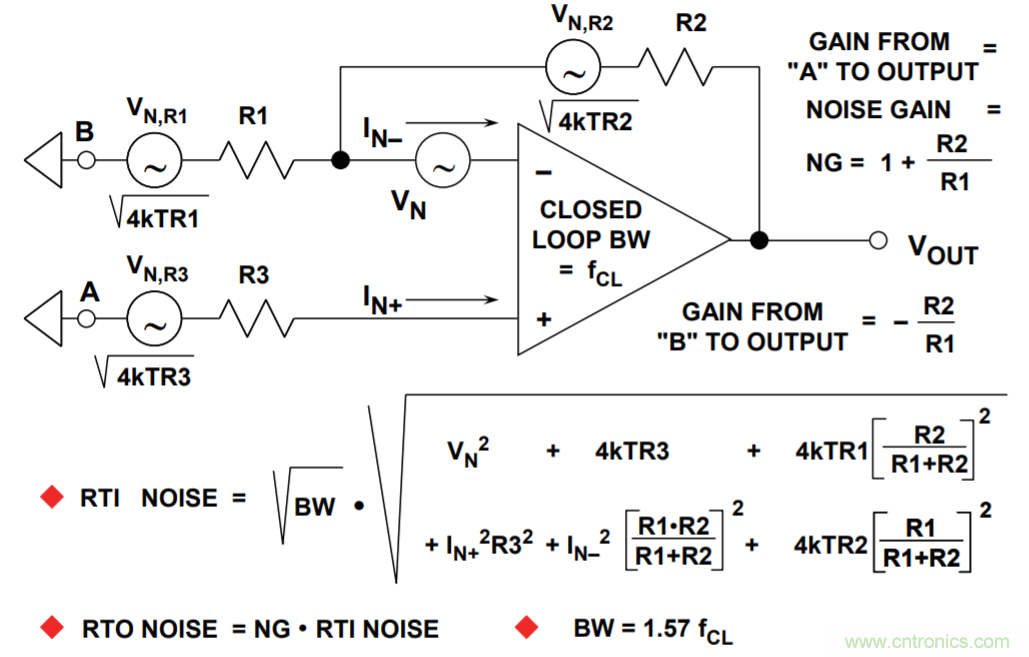
圖1:單極點系統(tǒng)的運算放大器噪聲模型
下圖2詳細分析了圖1中的各噪聲源是如何反映到運算放大器輸出端的。有關反相輸入端的電流噪聲效應,還需要進一步討論。此電流IN–不會按預期流入R1——放大器周圍的負反饋可使得反相輸入端的電位保持不變,因此從該引腳流出的電流在負反饋強制作用下僅能流入R2,從而產(chǎn)生IN– R2輸出端電壓。也可以考慮IN–流入R1和R2并聯(lián)組合產(chǎn)生的電壓,然后通過放大器的噪聲增益放大,但結果是一樣的,計算反而更復雜。
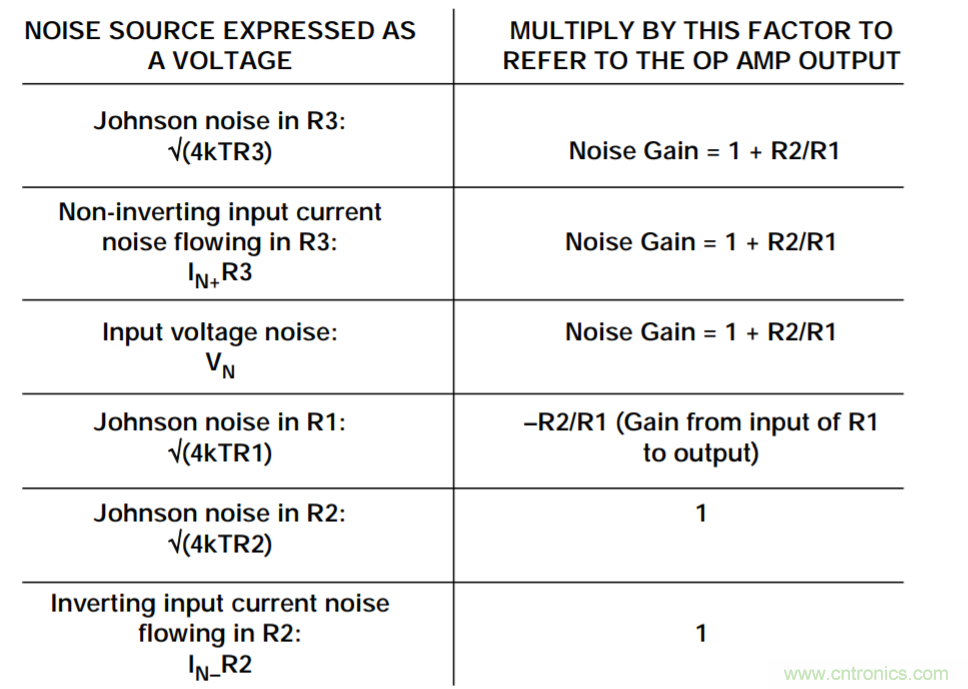
圖2:折合到輸出端的噪聲源(RTO)
請注意,與三個電阻相關的約翰遜噪聲電壓已包括在圖2的表達式中。所有電阻的約翰遜噪聲為√(4kTBR),其中k是玻爾茲曼常數(shù)(1.38×10–23 J/K),T是絕對溫度,B是帶寬(單位為Hz),R是電阻(單位為Ω)。一個很容易記住的簡單關系是:1000 Ω電阻在25ºC時產(chǎn)生的約翰遜噪聲為4 nV/√Hz。以上分析假設是單極點系統(tǒng),其中反饋網(wǎng)絡為純阻性,且噪聲增益與頻率關系曲線平坦。此情況適用于大多數(shù)應用,但如果反饋網(wǎng)絡包含電抗元件(通常為電容),則噪聲增益在目標帶寬內不恒定,必須使用更復雜的技術來計算總噪聲。有關二階系統(tǒng)噪聲的考慮,請參見指南MT-050。
參考文獻
1. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 1.
2. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 1.
推薦閱讀:







